Les ratios de brassage du système égyptien.
L’analyse des ratios de brassage mésopotamiens s’appuie sur des centaines de tablettes cunéiformes, des comptabilités au jour le jour de grains et d'ingrédients de brassage utilisés pour brasser diverses qualités de bière.
L’analyse des ratios de brassage égyptiens s’appuie sur deux papyrus d’exercices mathématiques, le papyrus Ahmès/Rhind et le papyrus Golenichtchev dit de Moscou, tous deux datés du Moyen Empire, respectivement la XIIè (1991–1778 BC) et la XIè (2150-1991 BC) dynasties. Ces deux documents énumèrent des problèmes arithmétiques, algébriques et géométriques, 91 pour le papyrus Ahmès/Rhind, 25 pour le papyrus de Moscou[1]. Seuls une partie des exercices arithmétiques concernent la question des ratios de brassage : 10 pour le papyrus Ahmès/Rhind, 10 pour celui de Moscou.
Ils traitent des moyens de comparer (ou d’échanger) une quantité donnée de bière contre une quantité équivalente de pain, et vice versa. Ou encore de convertir un volume donné de bière de telle densité en un autre volume de bière de densité différente. Ou encore de répartir un volume de bière de telle densité entre diverses personnes qui doivent recevoir de la bière de qualité (densité) distincte en fonction de leur rang social.
Ces calculs ont une évidente portée pratique. Les exercices sont destinés à l’entrainement mental des scribes qui doivent au quotidien faire de tels calculs pour contrôler l’utilisation des grains sortis des greniers. Ces grains sont convertis en malt (bcha, bš3  ), en bière (hnq.t
), en bière (hnq.t 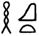 et variante
et variante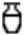 qui désigne aussi la jarre-dś pour la bière) ou en pain (pain à bière ou pain de boulangerie).
qui désigne aussi la jarre-dś pour la bière) ou en pain (pain à bière ou pain de boulangerie).
Calculer des rations de bière de diverses densités est aussi le travail du scribe. Il doit également savoir convertir un nombre de pains de tel poids en nombre de jarre de bière de telle densité sur la base des volumes de grains utilisés dans les deux cas. Il doit enfin recalculer la densité d’une bière contenue dans une jarre après sa dilution avec de l’eau.
Tous ces exercices ont pour horizon pratique la gestion des rations de bière et de pain attribuées aux équipes qui travaillent dans les ateliers ou les champs. Ces rations doivent respecter le rang social des bénéficiaires, comme en Mésopotamie. Un chef d’équipe ne reçoit pas la même quantité de grains, sous forme de bière et de pain, qu’un simple manœuvre.
Les problèmes arithmétiques dits « pefsu (ou pesu) » ont été analysés sous l’angle d’une économie égyptienne fonctionnant grâce aux échanges en nature, une économie de troc entre producteurs de céréales et institutions royales (palais, temples, sanctuaires) ou entre ces institutions elles-mêmes. L’aspect social a été sous-estimé. Les ratios de brassage sont plus que des recettes de brasseurs. Ils expriment le besoin de contrôler la densité de la bière rapportée aux volumes de grains utilisés. Ce volume de grains mesure exactement la part de grains accordée chaque jour ou chaque mois aux bénéficiaires des rations de bière. Cette part varie en fonction de leur statut social ou de leur place dans la hiérarchie d’une équipe de travailleurs.
Calculer la densité d’une bière, la part de grains contenue dans un volume donné de bière, garantit le respect effectif des hiérarchies sociales, sachant que toute la société égyptienne boit de la bière, du plus humble ouvrier jusqu’au pharaon. En Egypte, les ratios de brassage sont l’affaire des scribes plutôt que celle des brasseurs.
QUELS SONT LES OUTILS DU SCRIBE EGYPTIEN ?
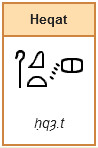
Pour évaluer et calculer la densité des bières, le scribe égyptien a besoin de trois unités : le hekat mesure un volume de grains, la jarre-dś mesure un volume de bière, le pefsu donne le rapport mathématique entre ces deux valeurs.
Le hekat (ou heqat) est l’unité égyptienne de volume utilisée pour mesurer des quantités de grain ou de bière. Il vaut 4.8 litres. Le hekat correspond au volume de grains qu'une pelle peut ramasser sur les aires de battage ou dans les greniers. Cette unité-référent suit toutes les opérations relatives aux grains : stockage, circulation, échanges et surtout transformation en pain ou en bière. Le hekat mesure des volumes de grains crus (orge, blé amidonnier), de malt, de farine, etc[2].
ds Faulkner p. 316, Wb. V p. 485, 3-15
-
cf. W22![D46 [d] d](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_D46.png)
![O34 [z] z](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_O34.png)

1 hekat = 3,75 kg ou 4,8 litres.
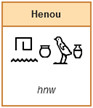
1 hekat = 10 hin (henou)
1 hekat = 64 dja
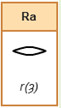
1 hekat = 320 ro (ra)
La jarre-dś ( ou pot à bière W22) est une jarre de contenance standardisée. Sans ce volume fixé et connu de tous, la mesure des densités de bière resterait un calcul théorique. De même, les problèmes de dilution de la bière avec de l’eau, ou de mélange entre orge et dattes pour la brasser, exercices proposés par le papyrus Ahmès/Rhind ou celui de Moscou n’auraient aucune application concrète[3].
Connaître la ou les capacités des jarres-dś reste la question cruciale. Sans cette donnée, on ne peut estimer la densité réelle des bières égyptiennes. Wolfgang Helck a proposé en 1971 une contenance entre 2½ et 3 litres[4].
Un exemplaire de jarre à bière avec bouchon d'argile (h. 30 cm diam ouverture 10.5 cm) datée de la 12ème dynastie (règne d'Amenemhat I) provient de Thèbes, Asasif sud, Tombe de Wah. Elle est contemporaine des sources qui sont à l'orgine des deux papyrus (Moyen-Empire ca. 1981–1975 B.C.). Elle contient environ 8 litres[5]. Une capacité oscillant entre 5 et 8 litres est incompatible avec une une jarre standardisée, du moins pour respecter des densités de moût de bière reflétant les calculs très précis des scribes (infra). Les jarres à bière utilisées dans les ateliers de brassage égyptiens ont une capacité plus élevée, environ 30 litres (jarre découverte dans le temple funéraire d'Amenemhat III, Dashur).
La jarre-dś sert aussi à recueillir du jus de dattes après pressage. Elle peut contenir 20 hin, soit environ 10 litres[6].
La question de la contenance de la jarre-dś n’est donc pas résolue. Les publications parlent tantôt de cruches-dś (0,5 litres), de pots-dś (5 litres) et les archéologues découvrent des jarres-dś (8 litres). Ces contenants à bière ont évolué pendant 3 millénaires. Ils ont aussi varié d’une région à l’autre. A côte de la jarre-dś, la jarre à bière ḏwjw (djouiou) a aussi servi de mesure pour la bière. Il existait sans doute une gamme standardisée de jarre-dś : petite, moyenne et grande jarre-dś, idem pour la jarre-ḏwjw. Les exemplaires de jarres à bière et les références textuelles à la jarre-ds proviennent en majorité de contextes funéraires (tombes et formulaires stéréotypés de listes d'offrandes). Les contextes liés à la distribution des rations de bière sont moins connus.
psw Faulkner p. 94, Wb. I p. 552, 8-11
Le pefsu (ou pesu, pfśw) mesure la densité de la bière, plus précisément la densité théorique du moût (sucres) avant sa fermentation.
Pefsu = nombre de jarres-dś de bière / nombre de hekat de grains.
10 jarres-dś de bière brassée avec 5 hekat de grains = 2 pefsu. 10 jarres-dś de bière brassée avec 10 hekat de grains = 1 pefsu. Plus le pefsu est élevé, plus la densité de la bière diminue. Le pefsu est aussi une unité de la pratique, pas seulement une valeur théorique. Les offrandes de bière ou les formulaires consacrés à l'entretien des personnes après la mort mentionnent le nombre de jarres-dś de tel pefsu[7].
Dans la pratique, le pefsu, ratio théorique de brassage, possède des valeurs très variables. W. Helck retient les pefsu de valeurs 1, 1½ et 2 comme d’usage courant dans les documents qui émanent des temples et des maisons royales. Il signale cependant que des ratios 2, 3, 4, 5, 10, 14, 20, 30, 40, 50, sont attestés pendant le Nouvel Empire (Helck 1971, 47). Un pefsu de 50 (1 hekat de grains pour 50 jarres-dś !) produit une bière extrêmement faible, presque de l’eau, quelle que soit le volume d’une jarre-dś. A l’inverse, un pefsu 1 dénote une bière très forte.
Un fait est acquis. Les ratios de brassage sont mis en œuvre dans l’ancienne Egypte pour respecter une hiérarchie sociale. Plus le pefsu est bas, plus la ou le bénéficiaire occupe un rang élevé. Les exercices arithmétiques proposés aux scribes par le papyrus Ahmès/Rhind le démontrent (infra, notamment le n° 65)[8] .
LE PAPYRUS AHMES/RHIND ET LA DENSITE DE LA BIERE.
Le problème n° 65 répartit 100 galettes de pains parmi une équipe de 10 hommes. Le chef d’équipe, le gardien et le batelier reçoivent double-ration. Il est ici question de pains, ailleurs de bière. Les rations tiennent compte de la hiérarchie au sein de l’équipe. La situation dans cette hiérarchie se mesure en volume de grains contenu dans les rations de pain et de bière : un pain plus ou moins gros, une bière plus ou moins forte.
Problème Ahmès/Rhind 65 : répartir des rations de pains entre 10 hommes.
Exemple de partage de 100 pains entre 10 hommes, dont un batelier, un contremaître et un portier, qui reçoivent des portions doubles. Quelle est la part de chacun ?
Le calcul. Ajoutes au nombre des hommes 3 [pour ceux qui ont des portions doubles] ; cela fait 13. Multiplie 13 de façon à obtenir 100 [100/13]; le résultat est 7 2/3 1/39. C'est la "ration alimentaire" pour sept des hommes, le batelier, le contremaître et le portier recevant la double [portion].
Pour preuve on ajoute 7 2/3 1/39 pris 7 fois et 7 2/3 1/39 pris 3 fois pour le batelier, le contremaître, et le portier. Le total est 100.
On peut augmenter le nombre de pains selon le niveau hiérarchique des bénéficiaires. On peut aussi augmenter le nombre de jarres à bière. Cependant, les exercices de calcul du pefsu liés à la bière montrent que le scribe va aussi jouer sur la densité de la bière : plus ou moins de grains pour le même volume de bière, dilution avec de l'eau, ajout de dattes et même remplacement partiel de l'orge par d'autres céréales comme le blé-amidonnier.
La dilution de la bière est une solution pratique pour adapter sa densité au rang social du bénéficiaire. Le problème 71 montre comment calculer le pefsu, la densité théorique, d’une bière diluée.
Problème Ahmès/Rhind 71 : dilution de la bière.
De 1 jarre-dś de bière, on a retiré ¼ de la bière, puis on a rempli la jarre d'eau. Quel est le pefsu de la bière diluée ?
Calcules la quantité de malt (besha) pour 1 jarre-dś de bière; elle est de ½ hekat. Enlèves-en 1/4, soit 1/8 hekat ; le reste est 1/4 1/8 hekat. Multiplies 1/4 1/8 hekat de manière à obtenir 1 hekat ; le résultat est 22/3 et c'est le pefsu.
La solution donnée par Ahmès est très instructive. On ne connait pas le pefsu initial de la bière dans la jarre-dś. Mais Ahmès nous dit « Calcule la quantité de malt (besha) pour 1 jarre-dś de bière; elle est de 1/2 hekat ». Dans l’exercice proposée, la jarre-dś de bière avant dilution valait 2 pefsu (1/0,5). Si on la dilue d’un quart, c’est comme si on ne l’avait brassée qu’avec1/4 1/8 du demi-hekat initial. Le rapport de 1/4 1/8 à 1 hekat est bien de 2 2/3 (1/0.375 = 2,66666... dans notre système décimal).
Initialement, la jarre-dś contient de la bière de pefsu=2, brassée avec ½ hekat de malt, soit 2,4 litres ou 1,8 kg de malt. Si on suppose que ce pefsu=2 correspond à un ratio technique 1:1 (rapport réel entre volume initial de malt et volume de moût obtenu), la jarre-dś contient environ 2,4 litres. Ce ratio technique (densité réelle du moût avant fermentation) correspond à une bière forte (voir ratios mésopotamiens).
Les bières de pefsu 1 sont deux fois plus fortes et sans doute réservées au sommet de la hiérarchie sociale égyptienne. Le pefsu 1 semble être la densité de bière la plus élevée rencontrée dans les documents égyptiens.
Le problème 77 documente un autre cas pratique, celui de l’échange de jarres de bière contre des pains à pefsu égal. Autrement dit sur la base du même volume de grains utilisé pour les confectionner. La « valeur » des rations se calcule sur le volume des grains, logique sociale qui s’applique aux équipes de rationnaires mais également entre personnes de rang social différent. En théorie, une personne peut ne recevoir que de la bière ou que du pain, du moment que le total des grains consommés sous cette forme correspond à son rang social.
Problème Ahmès/Rhind 77 : échange de jarres de bière contre du pain.
10 jarres-des de bière pefsu 2, sont à échanger uniformément contre aHa (x) miches de pain pefsu 5. Trouver aHa. aHa = 25. Calcules la quantité de farine-wedyet dans 10 jarres-ds de bière ; cela fait 5 hekat. Multiplies 5 par 5 ; cela fait 25. Dis alors qu'il faut 25 pains pour faire l'échange.
Il faut 5 hekat de malt pour brasser 10 jarres-ds de bière pefsu 2.
5 hekat de pains pefsu 5 => 25 miches de pains.
Fait-on en Egypte de la bière avec de la farine-wedyet ? Sans doute si elle sert à confectionner les pains à bière qui sont ensuite émiettés pour brasser. A noter que dans le calcul du pefsu, grains crus, malt, farine sont équivalents.
W. Helck a fait remarquer que les Egyptiens savaient retirer 1/31è du volume après mouture des grains (Helck 1971, 44). Une bière dont le pefsu est calculé sur un volume initial de malt est par conséquent plus riche que si on calcule avec des hekat de grains crus. Le maltage fait perdre environ 20% de volume aux grains entiers bruts. Même remarque pour l’emploi de la farine (1/31è ≈ 3%).
Le problème 78 documente le cas inverse du 77 : échange de pains contre des jarres de bière à pefsu égal. Ahmès introduit dans son énoncé le aHa, la valeur inconnue à calculer, l’équivalent de l’inconnue x dans nos équations algébriques.
Problème Ahmès/Rhind 78 : échange de pain contre des jarres de bière.
100 pains de pefsu 10 doivent être échangés uniformément contre aHa jarre-dś de bière de pefsu 2. Trouver aHa. aHa = 20 jarres-dś de bière.
Calcules la quantité de farine-wedyet dans 100 pains de pefsu 10 ; cela fait 10 hekat. Multiplies 10 par 2 ; cela fait 20. Disons alors qu'il faut 20 (jarres-)dś de bière pour faire l'échange.
LE PAPYRUS DE MOSCOU ET LA DENSITE DE LA BIERE.
Le papyrus de Moscou propose des exercices similaires. 10 exercices sur 21 sont des problèmes de pefsu. Parmi eux, les n° 5, 8, 9, 20 calculent le pefsu de pains, 12, 13, 14 et 16 le pefsu de jarres de bière, 22 et 24 des équivalences entre pains et jarres de bière de pefsu différents[9].
Les problèmes 9 et 13 sont similaires au Ahmès/Rhind 71 :
Problème Moscou 13 : dilution de la bière.
Soit une jarre-ds de 2 pefsu, quel sera le pefsu après dilution d'un quart de la bière ?
Réponse : la bière a demandé ½ hekat de grains moins ¼ (remplacé par de l'eau) = 3/8, soit la nouvelle valeur du pefsu = 8/3.
Les problèmes 22 et 24 répartissent de l’orge pour faire du pain et de la bière, les deux constituants fondamentaux des rations alimentaires égyptiennes :
Problème Moscou 22 : orge pour faire du pain et de la bière.
10 hekat d'orge de Haute-Egypte pour faire 100 galettes de pain et 10 jarres-ds de bière pefsu 2. Trouves le pefsu du pain.
10 jarres-ds de bière pefsu 2 = 5 hekat. 10 – 5 hekat pour 100 galettes => pefsu = 20.
Problème Moscou 24 : orge pour faire du pain et de la bière.
15 hekat d'orge de Haute-Egypte pour faire 200 galettes de pain et 10 jarres-ds de bière. Le pefsu de la bière est 1/10 celui du pain. Trouves le pefsu de la bière et celui du pain.
200 galettes pefsu 20, 10 jarrea-ds de bière pefsu 2.
Le problème 16 traite du remplacement de l’orge (ou du malt d’orge) par du blé-amidonnier. La formule « 3/4 n bš3 bnr »[10], littéralement 3/4 fois malt pour (1/4) datte, décrit la composition d’un type de bière et peut intervenir dans les calculs. Certains problèmes en tiennent compte et diminue de ¼ volume de grains nécessaires, d’autres l’ignorent pour calculer le pefsu. Ici le ratio orge/blé amidonner = 22/3. Une jarre-dś de bière pefsu 2 brassée avec ½ hekat d’orge devient une bière pefsu 2 brassée avec 0,375 hekat de blé amidonnier. Ainsi une jarre-dś de bière d'orge pefsu 2 peut se troquer contre 0,375 hekat de blé amidonnier, ou une jarre-dś de bière brassée avec ce dernier.
Problème Moscou 16 : bière de blé-amidonnier.
Une jarre-ds de bière pefsu 2 en échange de blé-amidonnier au rapport de 22/3. Trouves le blé-amidonnier.
1 jarre-ds de bière pefsu 2 (1/2 hekat) tu échanges pour 3/8 hekat de blé-amidonnier.
Le problème 12 est l’un des plus intéressants. Il se rapproche de Ahmès/Rhind 71 ou Moscou 13 (dilution de la bière), mais cette fois la bière est brassée avec du malt et des dattes à part égales. Le calcul de la densité théorique finale se complique un peu et fait intervenir un ratio de densité entre l'orge et le mélange malt-dattes.
Problème Moscou 12 : bière mi-malt mi-dattes.
13 hekat d'orge de Haute-Egypte pour faire 18 jarres-ds de bière mi-malt mi-dattes (bš3 mì bnr), malt idem [même qté 13 heqat] dattes pefsu 21/6. Pefsu final de la bière = 3. Pourquoi ?
Solution : le mélange malt-dattes vaut 6 hekat (13 hekat orge / pefsu 21/6 = 6). Donc 18 jarres/6 hekat-équivalent-malt-dattes = 3 pefsu.
Ces deux derniers problèmes font sentir les limites pratiques du système égyptien. Dès que la bière se compose d'ingrédients hétérogènes, des informations complémentaires sont requises. Elles diront par exemple que le malt vaut 22/3 du blé-amidonnier (prob. 16), ou que le ratio orge/mélange mi-malt-mi dattes vaut 21/6 (prob. 12).
D’où proviennent ces deux derniers ratios ? Les calculs de pefsu ne font intervenir ni processus de fabrication (durée, travail, matériels), ni qualité issue de la transformation des ingrédients (orge et malt d’orge sont équivalents). Seule la nature des matières premières est prise en compte, d’où les ratios entre orge, blé et dattes. Charles Nims (1957) a interprété ces proportions comme des barèmes commerciaux ou des valeurs conventionnelles pour le troc. Cette explication n’est pas incompatible avec une logique sociale des ratios fondée sur l’équivalence volume de grain (bière et pain) ⇔ rang social. Les bières brassées en partie avec des dattes requièrent un ratio supplémentaire pour comparer un volume de dattes et un volume d’orge et ramener le pefsu à un volume théorique de grains.
GRILLES des STATUTS SOCIAUX ⇔ RATIOS DE BRASSAGE (PEFSU).
Ostracon provenant de Deir el-Medineh. 280 jours de travail enrgistrés, dont le brassage de la bière. Année 40 de Ramses II (r. 1279-1213 av. n. ère), verso BM EA5634.
Année 40 de Ramses II (r. 1279-1213 av. n. ère), verso BM EA5634.
De nombreuses listes de distributions de rations illustrent l’équivalence entre statut social et bénéfices alimentaires. La proportionnalité est quantitative : plus de pains et de jarres de bière par personne pour l’entourage royal du palais ou les chefs de sanctuaire par exemple que pour le portier ou le simple serviteur (Helck 1971, 55-62).
A notre connaissance, nous n’avons pas pour l’Egypte de textes de distributions de rations illustrant une équivalence qualitative. Par exemple une densité de bière plus forte (pefsu 1) pour le sommet de la hiérarchie et plus faible (pefsu 2 à 4 voire moins) pour les plus humbles.
Les pefsu de valeurs très basses (20, 30, 40, …) signalés par (Helck 1971, 49) sont attestées au Nouvel Empire et mis en œuvre lors de fêtes collectives réunissant un grand nombre de personnes. Brasser une grande quantité de bière implique alors sans doute de diminuer drastiquement sa densité.
Le site de Deir el-Medineh, près de Thèbes, abritait un village d’ouvriers spécialisés dans la construction et l’entretien des nécropoles royales du Nouvel-Empire (c. 1550 BC–c. 1077 BC). Les archéologues ont retrouvé des comptabilités de rations rédigées sur des morceaux de calcaire, des tessons de poteries ou du papyrus. Les rations mensuelles de grains (amidonnier + orge) font clairement apparaître des différences de statut[11].
| Rations d’amidonnier et d’orge (litres) des équipes travaillant à Deir el-Medineh, d'après Janssen 1997, 14-15. | ||||
| Amidonnier | Orge | Total mois | Total jour | |
| Chef équipe, scribe | 528 | 192 | 720 | 24 |
| Ouvrier | 384 | 144 | 528 | 17,6 |
| Garde | 312 | 120 | 432 | 14,4 |
| Femme esclave | 144 | 144 | 288 | 9,6 |
| Jeune homme | 144 | 48 | 192 | 6,4 |
| Portier | 96 | 48 | 144 | 4,8 |
| Docteur | 96 | 24 | 120 | 4 |
Ces rations nourrissent le titulaire mais également sa famille qui habite sur place. Les grains servent à faire du pain et brasser de la bière. Au regard des différences de volume entre le chef d’équipe + le scribe et les ouvriers, le surplus de grains (+40%) attribué aux premiers permet de brasser des bières plus fortes. Certains ostraca de Deir el-Medineh racontent les jours d’absence pour brasser la bière suivis de beuveries (Janssen 1980, SAK 8. Grandet 2002, cat. 113). Nous n’avons malheureusement aucune information sur la densité de ces bières.
COMPARAISON AVEC LES RATIOS DE BRASSAGE MESOPOTAMIENS.
Confronté à la même situation, la production massive de bières contrôlée par des magasins de grains et des ateliers de brassage centraux, le scribe mésopotamien adopte une démarche similaire : ne contrôler que les entrées-sorties. Il ne comptabilise que les grains qui entrent dans la brasserie et les jarres de bière qui en sortent.
Le scribe égyptien crée le pefsu, unité théorique égale au nombre de pains ou de jarres de bière obtenus avec 1 hekat de grains. Sa formule est : x jarres (ou x pains) /y hekat = z pesu. Il fonctionne donc comme la plupart des ratios mésopotamiens (bières ½ ta, 1 ta, 1½ ta, 2 ta, …) et repose, comme eux, sur la standardisation de la taille des pains ou de la contenance des jarres : jarre-dś égyptienne et jarre-piḫum (ou jarre-dida) mésopotamienne.
Une différence sépare néanmoins le pesu égyptien et le ratio de brassage mésopotamien.
Jarre découverte dans le temple funéraire d'Amenemhat III (-1842 à -1797), à Dashur. ≈ 30 litres.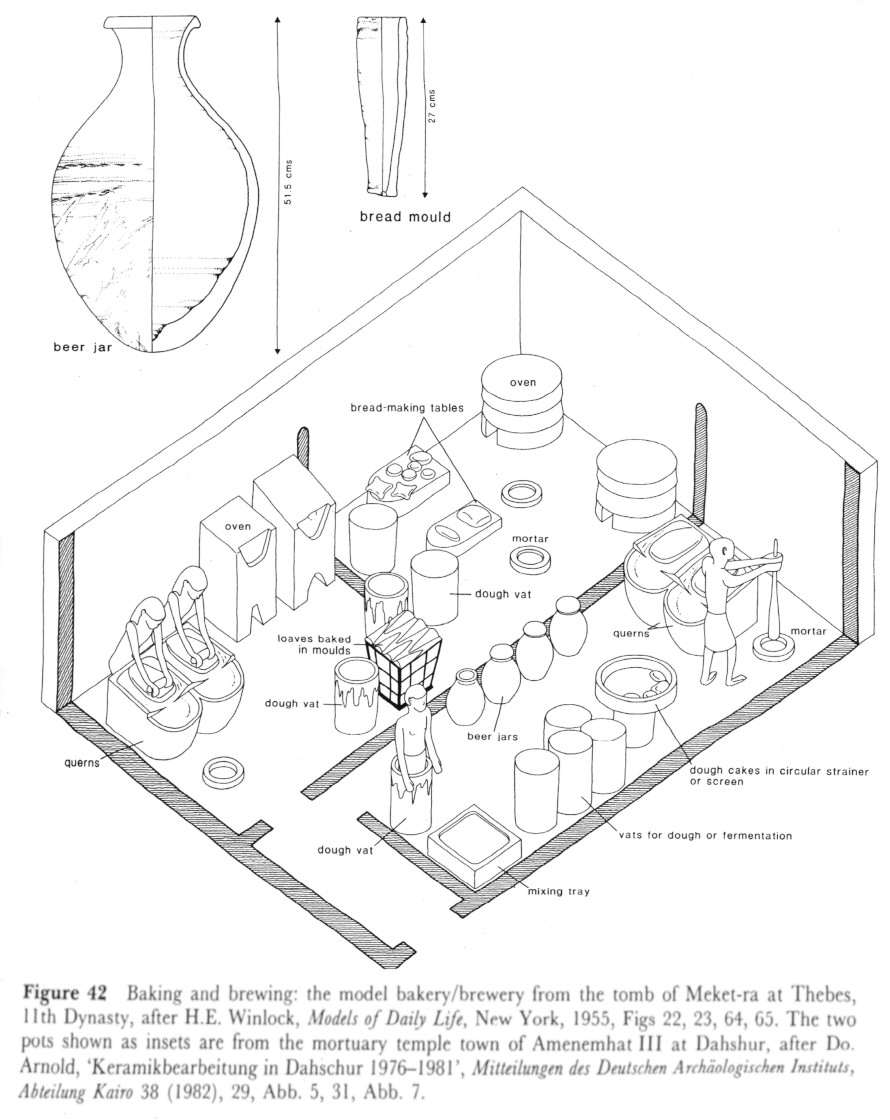 Modèle réduit en bois : cuisson du pain et brassage de la bière (Kemp fig. 42 d'après Winlock 1955).
Modèle réduit en bois : cuisson du pain et brassage de la bière (Kemp fig. 42 d'après Winlock 1955).
Ce dernier n'atteint pas le degré de généralité pratique et théorique du premier. Le scribe égyptien utilise le pesu pour convertir et comparer tous les produits à base de grains (pains, galettes, malt, bière), mais également les dattes et d'autres aliments comme l'huile ou la graisse. Le pesu figure également comme véritable unité de calcul dans des exercices mathématiques destinés aux apprentis-scribes.
Cependant, la gestion concrète de chaque sorte de bière s'appuie sur des notations conventionnelles mais aussi sur des contrôles réels sur le terrain.
Est-ce la raison qui a empêché le pragmatique gestionnaire mésopotamien de se forger son unité théorique de calcul pour la bière ?
Gestionnaires de brasserie égyptiens et mésopotamiens apportent au même problème une solution différente. Il serait intéressant de connaître les facteurs qui ont gouverné ces choix. Le pesu égyptien trouve son application pratique dans le troc. Une jarre dś à 1 pesu s'échange contre 1 pesu d'autres produits et selon des barèmes définis : 3/8 hekat de blé-amidonnier, 2/3 de dattes, 3/2 de malt ou encore 1 pesu de galettes.
Une trop grande variété de bières a-t-elle freiné, en Mésopotamie, des modes équivalents de calcul ? Les notations 1 (jarre)-piḫum ou 1 (jarre)-dida impliquent leurs équivalents-orge dans l'esprit du gestionnaire mésopotamien, mais l'information reste implicite et dépendante dans tous les cas de chaque type de bière, connu de celui seul qui a la jarre entre les mains. Quant au troc des jarres de bière contre d'autres produits, il s'appuie sur des barèmes courants et connus de tous. Ils se rapportent tous au volume d'orge, la denrée de référence. Nul besoin de fixer une unité théorique d'échange. Les grands marchands mésopotamiens procèdent de la même manière et convertissent la valeur d'une marchandise soit en orge, soit en argent, soit en étain dans le Nord. Le besoin d'une unité abstraite de référence comme le pesu égyptien, relevant de la pratique des scribes, ne s'est pas fait sentir.
Atelier de brassage. 13 ouvriers à la mouture, 9 criblant la farine, 4 acroupis devant des fours, 3 brassant la maische dans des cuves, un surveillant. Modèle réduit en bois d'un atelier de brassage, Thèbes, 11ème Dynastie, BM EA40915.
Modèle réduit en bois d'un atelier de brassage, Thèbes, 11ème Dynastie, BM EA40915.
Reste, à côté des habitudes scribales, la pratique du brasseur. Il ne dispose que du matériel d'usage courant – paniers, pots, vases, cuves ou récipients plus ou moins standardisés – pour mesurer ses matières premières, le moût et la bière finie. Ustensiles standardisés, pragmatisme et recette prédéfinie épargnent au brasseur des mesures précises et de savants calculs, deux techniques concrètement hors de sa portée[12].
Cette façon de procéder implique qu'à un brassin correspond une seule qualité ou densité de bière.
Pour le brasseur, un brassin est l'unité d'œuvre minimale, le processus par lequel il engage tel volume de grains pour produire tel volume de bière d'une qualité définie. Du même versement de grains et d'ingrédients ne sortent pas une bière supérieure et une bière diluée obtenue par lavage des drêches, comme on l'a parfois supposé. Ceci obligerait le brasseur à de complexes calculs pour ventiler le volume initial de grains en une double sortie de deux bières possédant des ratios différents. Ceci l'obligerait à prendre des leçons de son confrère égyptien pour manipuler le pesu (voir les problèmes de dilution de la bière) !
C'est pourquoi les relevés comptables mésopotamiens font toujours correspondre tel volume de grains avec tel volume final d'une seule qualité de bière pour ne pas déroger à la logique du ratio de brassage. Le brasseur égyptien, ou le scribe, semble au contraire capable de diluer le moût pour obtenir une densité plus faible dont il sait calculer la valeur exprimée en pefsu.
BIBLIOGRAPHIE
Chace Buffum Arnold, Ludlow Bull, Henry Parker Manning, The Rhind Mathematical Papyrus. Volume I, 1927. archive.org/details/arnoldbuffumchaceludlowbullhenryparkermanningtherhindmathematicalpapyrus.volumei
Clagett Marschall, Ancient Egyptian Science. A Source Book. Volume Three. Ancient Egyptian Mathematics. 1999. books.google.fr/books?id=8c10QYoGa4UC&pg=PA60&lpg=PA60&dq=pefsu...
Grandet Pierre, Les artistes de Pharaon. Deir el-Medineh et la Vallée des Rois (Catalogue exposition du Louvre 2002).
Grandet Pierre, Le Papyrus Harris I (BM 9999) 1-2, Bibliothèque d'Etude (Publication de l'IFAO) = BdE 109/2, 1994.
Helck Wolfgang, Das Bier im Alten Ägypten, Gesellschaft für die Geschichte und Bibliographie des Brauwesens E.V., Berlin 1971. Helck 1971
Janssen Jac, Village Varia. Ten Studies on the History and Administration of Deir el-Medina, Nederlands Insituut voor het Nabije Oosten, Leiden 1997.
Janssen Jac, Absence from work by the necropolis workmen of Thebes. Studien zur Altägyptischen Kultur (SAK 8), 1980, 127-152.
Kemp Barry J. , Ancient Egypt. Anatomy of a civilization. Routledge 1989 (réimp. 1991). archive.org/details/BarryJ.KempAncientEgyptAnatomyOfACivilibOk.org
Nims Charles, The bread and beer problems of the Moscow mathematical papyrus, Journal of Egytian Archaeology 44, 1958, 56-65. jstor.org/stable/3855065
Powel Marvin, Ancient Mesopotamian Weight Metrology: Methods, Problems and Perspectives, in Studies in Honor of Tom B. Jones, Alter Orient und Altes Testament 203, 1979, 71-110
Robbins G. & Shute C., The Rhind Mathematical Papyrus: an ancient Egyptian Text, 1987, 50-52.
Spalinger Anthony, Dates in ancient Egypt, (Studien zur Altägyptischen Kultur 15), 263-267. jstor.org/stable/44324591
Struve Vasiliĭ Vasilʹevich, Mathematischer Papyrus des Staatlichen Museums der schönen Künste in Moskau. in Quellen und studien zur gescichte der mathematik, abt. A: Quellen. bd. 1. 1930.
NOTES
[1] 20 problèmes si on élimine les exercices illisibles et fusionne 3 paires d’exercices très similaires.
[2] Sur les unités hekat et pefsu, B. Kemp "Ancient Egypt", 123-126. Et la logique des rations ibid. 117-120. B. Kemp évoque p. 124 la standardisation nécessaire des jarres à bière : "Many ration lists have survived. They tend to ignore the pefsu values. They assume standardized jugs of beer, and the various kinds of bread can be grossed together as 'mixed' loaves. This assumes standardization, a reasonable step in thinking in view of the scale and ubiquity of the operations, in which those involved, including potters making beer jugs, would tend naturally to produce standardized shapes from a lifetime's pratice." B. Kemp décrit comment les rations évoluent en quantité selon le rang social (p. 125-126) - nombre de pains ou de jarres de bière. Il n'envisage pas que les rations de bière puissent aussi varier selon la densité de la boisson. Cette technique résout un écueil biologique : une personne ne peut pas boire des cruches entières de bière en proportion de son rang social !
[3] Le caractère utilitaire des mathématiques égyptiennes n’est pas toujours mis en évidence par les égyptologues qui analysent ses formules du point du vue de l’histoire des mathématiques et la compare aux mathématiques grecques. Les études du papyrus Ahmès/Rhind portent presque exclusivement sur la géométrie et l'algèbre. L'arithmétique des problèmes dits "pesu" ou "pefsu" est jugée trop élémentaire. La publication en allemand du papyrus de Moscou par V.V. Struve en 1930, préparée par une étude de Touraev en 1912-1920. Struve reconstitue le texte et y ajoute une traduction avec un commentaire philologique et mathématique détaillé. La publication témoignait de l'importante connaissance scientifique théorique des Égyptiens, anticipant les réalisations de la science grecque (Struve biographie).
[4] Helck Wolfgang, Das Bier im Alten Ägypten, 1971. pp. 43-51 « Stärke und Arten des altägyptischen Bieres“, et spécialement p. 46. Voir aussi pp. 22-23 pourquoi bcha (bš3) désigne le malt (et non une "farine ou sorte de grain avec des fruits" !). En définitive, il faut se référer à l'analyse scientifique effectuée par Delwen Samuel avec des restes de bière retrouvés à Armana-Egypte.
[5] Contenance d’une jarre ovoïde = Rmoyen2 * H * 3,14. Rayon moyen = 9,25 cm. 9,25 * 9,25 * 30 * 3,14 = 8.060 cm3. Référence de la jarre Met 20.3.256a–c. www.metmuseum.org/art/collection/search/572197
[6] Grandet Pierre, Le Papyrus Harris I (BM 9999) 1-2, BdE 109/2, 1994, p. 80.
[7] Sur les unités hekat et pesu, B. Kemp, "Ancient Egypt", 123-126.
[8] Enoncé des problèmes d’après Arnold Buffum Chace, Ludlow Bull, Henry Parker Manning, The Rhind Mathematical Papyrus. Volume I, 1927.
[9] Charles Nims (1958) ne compte que 20 problèmes car 1 et 2 sont illisibles, 8 et 9 sont réunies, ainsi que 11-12, et 15-16.
[10] Charles Nims, The Bread and Beer Problems of the Moscow Mathematical Papyrus, JEA 44, 1958, pp. 56-59. Les scribes différencient l'orge et le blé-amidonnier avec la couleur de l'encre, l'orge tracé en noir, le blé-ammidonnier en rouge.
[11] Le chef d’équipe et le scribe reçoivent chacun 5½ khar (1 khar=96 l.) d’amidonnier et 2 khar d’orge / mois, chaque ouvrier 4 + 1½, jeune homme 1½ + 1, garde 3¼ + 1¼, portier 1 + ½, docteur 1 + ¼, femme esclave 1½ + 1½ (Janssen, 1997, 13-15).
[12] M. Powell (1979, 88-89) a montré le fossé existant entre les pratiques techniques et commerciales courantes mésopotamiennes, utilisatrices de poids et mesures d'une part, et l'extraordinaire développement des mathématiques babyloniennes d'autre part, réservées aux problèmes abstraits de calcul (comptabilité, astronomie, conversion des unités de mesure, exercices scolaires).




![S29 [s] s](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_S29.png)
![Z4 [y] y](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_Z4.png)


![Q3 [p] p](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_Q3.png)
![I9 [f] f](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_I9.png)
![G43 [w] w](https://www.hierogl.ch/h/extensions/wikihiero/img/hiero_G43.png)


